C# 11 was released on November 8th along with .NET 7, during the .NET conference, and generic math support is one of the important features that came out with it. Apart from this feature, it came with a lot of performance improvements and new features.
In this blog post, I am going to focus mainly on generic math support and related features.
Generic math support
The generic math support internally uses the generic interface and default methods of the interface. The default method of the interface was something that came out with C# 8. And I covered this in one of my YouTube videos as a part of C# 11 as well as my blog post here.
As a part of C# 11 enhancements, the methods of an interface can also be declared as abstract which was not the case before. To demonstrate the generic math feature I’ll take an example of a simple math problem that is nothing but adding two numbers.
Implementation without Generic math support
So to demonstrate that I am going to create a new method called Add. And for this method, I’ll just focus on adding two integers number for the time being.
int Add(int first, int second)
{
int result = 0;
result = first + second;
return result;
}
Above I declared Add method, which returns an integer. And this Add method is going to take two integer parameters, int first and int second.
Inside the method, I’ll declare a result variable of type integer, and I’ll set the initial value as 0. And then I’ll set the result variable as an addition of the first and second and then finally I’ll return the result.
Note, here the result variable might seem unnecessary but it will become interesting when I get to show the C# 11 feature.
Next, I will call this method and print the output to the console. To achieve that, I will create a new variable result, and assign the output of the Add method of two integer numbers 1 and 2 to the result. And finally, I will call the Console.WriteLine to print the result to the console.
var result = Add(1, 2);
Console.WriteLine(result);
If I run this program now, I am going to see output 3 printed in the console as expected.
Trying generic method
But let’s say for a change in requirement, the parameters of the Add method can be either a double or an integer. Now if I change the call to the Add method with double parameters from integers, and it will start failing as expected. Because the Add method takes two integer parameters.
At this point, I can make the Add method a generic method. But if I make this a generic method, it will cause an issue that we could not solve till C# 10.
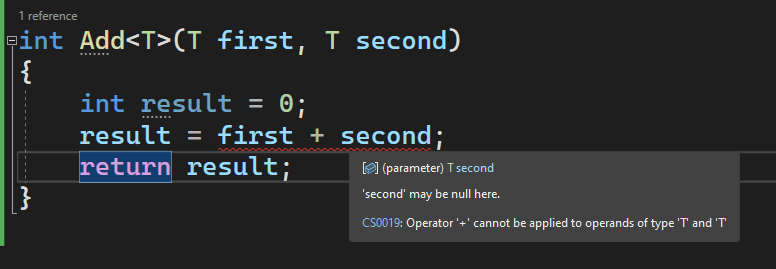
int Add<T>(T first, T second)
{
int result = 0;
result = first + second;
return result;
}
In the above change, when I change the integer parameters to a generic type T, the + operation will fail. And the reason for this error is “Operator ‘+’ cannot be applied to operands of type ‘T’ and ‘T'”.
And the second problem, we are returning the result as an integer, at this point, the result needs to be also of type T and so is the return type.
T Add<T>(T first, T second)
{
T result = 0;
result = first + second;
return result;
}
At this point, another issue that will arise is that we cannot set 0 to T. So these are the two problems we need to solve. And this is where exactly the new feature of C# 11 comes into play.
Using the generic math feature of C# 11
To solve the above issue we will use the INumber<T> interface, which is a generic interface available as a part of C# 11. So now if I update the code using the generic INumber interface, it will look like the below implementation.
The INumber interface is part of the System.Numerics namespace.
using System.Numerics;
T Add<T>(T first, T second) where T : INumber<T>
{
T result = 0;
result = first + second;
return result;
}
In the above code, I added a constraint for T as INumber<T>. And once I do that the error for the + operator for the generic type will no longer be there. And now if I hover over the + operator the help will show that “Adds two values together to compute their sum.”.
If I go into the definition of INumber, I will see that INumber derives from INumberBase. And INumberBase is something that implements another interface called IAdditionOperators. And IAdditionOperators is something that implements the plus operator.
public interface INumber<TSelf>
: IComparable,
IComparable<TSelf>,
IComparisonOperators<TSelf, TSelf, bool>,
IModulusOperators<TSelf, TSelf, TSelf>,
INumberBase<TSelf>
where TSelf : INumber<TSelf>?
public interface INumberBase<TSelf>
: IAdditionOperators<TSelf, TSelf, TSelf>,
IAdditiveIdentity<TSelf, TSelf>,
IDecrementOperators<TSelf>,
IDivisionOperators<TSelf, TSelf, TSelf>,
IEquatable<TSelf>,
IEqualityOperators<TSelf, TSelf, bool>,
IIncrementOperators<TSelf>,
IMultiplicativeIdentity<TSelf, TSelf>,
IMultiplyOperators<TSelf, TSelf, TSelf>,
ISpanFormattable,
ISpanParsable<TSelf>,
ISubtractionOperators<TSelf, TSelf, TSelf>,
IUnaryPlusOperators<TSelf, TSelf>,
IUnaryNegationOperators<TSelf, TSelf>
where TSelf : INumberBase<TSelf>?
public interface IAdditionOperators<TSelf, TOther, TResult>
where TSelf : IAdditionOperators<TSelf, TOther, TResult>?
{
/// <summary>Adds two values together to compute their sum.</summary>
/// <param name="left">The value to which <paramref name="right" /> is added.</param>
/// <param name="right">The value which is added to <paramref name="left" />.</param>
/// <returns>The sum of <paramref name="left" /> and <paramref name="right" />.</returns>
static abstract TResult operator +(TSelf left, TOther right);
/// <summary>Adds two values together to compute their sum.</summary>
/// <param name="left">The value to which <paramref name="right" /> is added.</param>
/// <param name="right">The value which is added to <paramref name="left" />.</param>
/// <returns>The sum of <paramref name="left" /> and <paramref name="right" />.</returns>
/// <exception cref="OverflowException">The sum of <paramref name="left" /> and <paramref name="right" /> is not representable by <typeparamref name="TResult" />.</exception>
static virtual TResult operator checked +(TSelf left, TOther right) => left + right;
}
Another point to note here as you can, the method of an interface can be abstract. And the method of an interface can be virtual as well. These are new additions in C# 11.
Zero for generic types
But in the above code, we still have an issue with the generic result set to 0. It is still throwing an error “cannot implicitly convert type ‘int’ to ‘T'” as expected.
To solve this problem, we can use another feature of C# 11 which came with generic math support. And that is using the Zero property of the INumber<T> on the generic type itself. And this Zero property gets the value 0 of the type.
The zero here is the zero equivalent for whatever numeric type is available in the generic type.
using System.Numerics;
T Add<T>(T first, T second) where T : INumber<T>
{
T result = T.Zero;
result = first + second;
return result;
}
At this point, all the errors from the Add method are gone. And this is due to the generic method support of C# 11.
Conclusion
Now if I run the application using doubles, or integer parameters, it will work in both cases.
var result = Add(1, 2);
Console.WriteLine(result);
The above code will result in 3.
var result = Add(1, 2.1);
Console.WriteLine(result);
And the above code now will result in 3.1 as expected. We are now able to add two double numbers as well as two integer numbers using generic math support.
My YouTube video on this topic is available here.